In mathematics and physics, vectors are powerful tools used to describe quantities that have both magnitude and direction. Unlike simple numbers, which only tell us “how much,” vectors also tell us “which way.” This makes them essential in subjects such as mechanics, engineering, navigation, computer graphics, and even everyday problem-solving like determining displacement or force. Among the basic operations involving vectors, vector subtraction plays a crucial role. While it may appear similar to ordinary subtraction at first glance, vector subtraction has its own logic, rules, and geometric meaning that make it unique.
This article provides a detailed, human-style explanation of vector subtraction, starting from foundational ideas and gradually moving toward deeper conceptual understanding. Rather than relying on memorized formulas alone, we will explore why vector subtraction works the way it does, how it can be visualized, and how it applies to real-world situations. By the end, you should feel confident not only performing vector subtraction but also understanding its significance.
What Is a Vector?
Before discussing vector subtraction, it is important to clearly understand what a vector is. A vector is a quantity defined by two main characteristics:
- Magnitude – how large or strong the quantity is
- Direction – the orientation in space in which the quantity acts
Examples of vectors include displacement, velocity, acceleration, force, and momentum. For instance, saying “a car moved 10 kilometers” is incomplete because it does not specify direction. Saying “a car moved 10 kilometers east” describes a vector because it includes both magnitude (10 km) and direction (east).
Vectors are often represented graphically as arrows. The length of the arrow represents the magnitude, and the arrowhead indicates the direction.
Scalar Quantities vs Vector Quantities
To better appreciate vector subtraction, it helps to compare vectors with scalars. Scalars are quantities that have magnitude only. Examples include mass, temperature, time, and distance. Subtracting scalars is straightforward: you simply subtract one number from another.
Vectors, however, cannot be subtracted using simple arithmetic alone because direction matters. Subtracting one vector from another means finding a new vector that represents the difference in both magnitude and direction.
The Basic Idea of Vector Subtraction
At its core, vector subtraction answers the question:
What vector must be added to one vector to obtain another vector?
Mathematically, if we have two vectors A and B, then:
A − B means finding a vector that, when added to B, gives A.
This interpretation is extremely important because it links vector subtraction directly to vector addition.
Vector Subtraction as Addition of the Negative Vector
One of the most fundamental principles of vector subtraction is that subtracting a vector is the same as adding its negative.
The negative of a vector has the same magnitude as the original vector but points in the opposite direction.
So,
A − B = A + (−B)
This idea allows us to convert subtraction problems into addition problems, which are often easier to visualize and solve.
For example, if vector B points north, then −B points south with the same length. Subtracting B from A means adding a vector that points opposite to B.
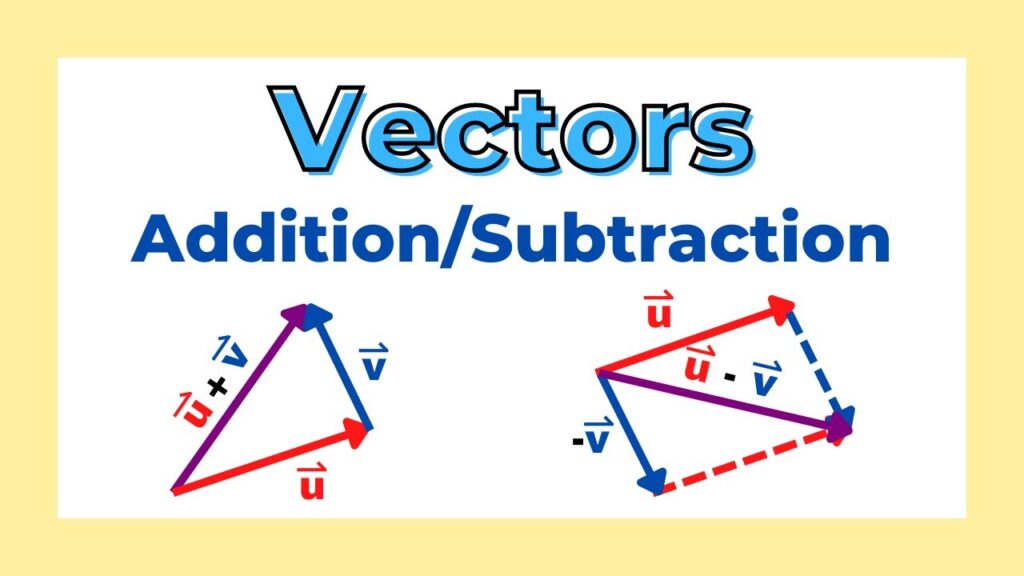
Geometric Representation of Vector Subtraction
Vector subtraction is best understood visually. There are two main geometric methods used to represent it.
1. Tail-to-Tail Method
In this method, both vectors are drawn starting from the same point (their tails coincide). The vector A − B is represented by the arrow that starts at the tip of B and ends at the tip of A.
This method emphasizes the idea of “difference” between the two vectors.
2. Head-to-Tail Method Using Negative Vectors
Here, vector A is drawn first. Then the negative of vector B (−B) is drawn starting from the head of A. The resultant vector from the tail of A to the head of −B represents A − B.
This method directly applies the rule that subtraction is equivalent to adding the negative.
Algebraic Method of Vector Subtraction
Vectors can also be represented using components, especially in two-dimensional or three-dimensional space.
For example, a vector A can be written as:
A = (Ax, Ay)
and vector B as:
B = (Bx, By)
To subtract B from A, we subtract their corresponding components:
A − B = (Ax − Bx, Ay − By)
This method is particularly useful in physics and engineering because it allows for precise numerical calculations and works easily in higher dimensions.
Vector Subtraction in One, Two, and Three Dimensions
One-Dimensional Vector Subtraction
In one dimension, vectors lie along a straight line. Direction is usually represented using positive and negative signs. For example, motion to the right may be positive, while motion to the left may be negative. Subtracting vectors in one dimension is similar to subtracting signed numbers.
Two-Dimensional Vector Subtraction
In two dimensions, vectors have both horizontal and vertical components. Subtraction involves dealing with both components simultaneously. This is common in problems involving displacement on a plane, such as navigation or projectile motion.
Three-Dimensional Vector Subtraction
In three dimensions, an additional component is included, often representing height or depth. This is essential in fields like physics, robotics, and computer graphics.
Physical Meaning of Vector Subtraction
Vector subtraction is not just a mathematical operation; it has deep physical meaning.
Relative Displacement
If one object is at position vector A and another is at position vector B, then A − B represents the displacement from B to A. This tells us how to move from one object to the other.
Relative Velocity
In physics, the velocity of one object relative to another is found using vector subtraction. If VA is the velocity of object A and VB is the velocity of object B, then:
Relative velocity of A with respect to B = VA − VB
This concept is crucial in understanding motion, especially in systems involving multiple moving objects.
Change in Velocity
Acceleration is defined as the change in velocity over time. The change in velocity is found by subtracting the initial velocity vector from the final velocity vector. Once again, vector subtraction provides the answer.
Common Mistakes in Vector Subtraction
Many learners struggle with vector subtraction due to a few common misunderstandings:
- Ignoring direction – Treating vectors like scalars leads to incorrect results.
- Incorrect negative vectors – Reversing magnitude instead of direction.
- Mixing up components – Subtracting the wrong components or using incorrect signs.
- Poor visualization – Not drawing vectors clearly can cause confusion.
Understanding the conceptual basis of vector subtraction helps avoid these errors.
Vector Subtraction in Real Life
Vector subtraction appears more often in daily life than we might realize.
- Navigation: Determining the shortest route between two locations.
- Sports: Calculating the change in velocity of a ball after impact.
- Engineering: Finding forces acting in opposite directions.
- Aviation: Determining wind effect on an aircraft’s actual path.
In each case, the difference between two vector quantities provides meaningful information.
Why Vector Subtraction Matters
Vector subtraction is essential because it allows us to compare vector quantities in a meaningful way. It helps us understand how one vector relates to another, not just in size but in direction as well. Without vector subtraction, many physical laws and engineering principles would be impossible to express accurately.
Conceptual Summary
- Vector subtraction finds the difference between two vectors.
- It is equivalent to adding the negative of a vector.
- It can be performed graphically or algebraically.
- It has deep physical significance in motion and force analysis.
- Proper understanding requires attention to both magnitude and direction.
Conclusion
Vector subtraction is a foundational concept that connects mathematics to the real world. While it may seem abstract at first, its logic becomes clear once we understand vectors as directional quantities rather than simple numbers. By viewing subtraction as the addition of a negative vector, using geometric visualization, and applying component methods, vector subtraction becomes both intuitive and practical.
Whether you are studying mathematics, physics, or engineering—or simply trying to understand how objects move and interact—mastering vector subtraction provides a strong base for more advanced topics. More importantly, it trains the mind to think spatially and logically, skills that are valuable far beyond the classroom.